Trigonometric Ratios

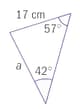
What information leads you to use the cosine rule.

What information needs to be given in order to be able to use the sine rule?

Which measurements can you calculate? What rule will you see? Explain your selection.

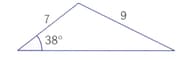
How do the sine rules and cosine rules help define the space we live in?

Which rule is more useful, the sine rule or the cosine rule.

Does it matter which version do you use?

Which version do you think easier to use to find an unknown angle?

How is the cosine related to Pythagoras theorem. Explain?

Explain why it is possible to rewrite the formula as $a^2=b^2+c^2-2bc\cos A$ so that it uses angle $B$ as $b^2=a^2+c^2-2ac\cos B$.

Rewrite the formula so that it uses angle $C.$

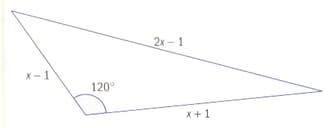
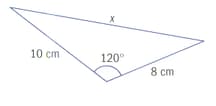
Explain why you cannot use the sine rule to find the length $x$ in this triangle.

Circles of radius $10\text{ cm}$ and $6 \text{cm}$ overlap as shown:

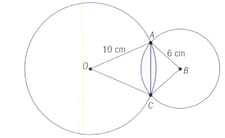
The circles meet at point $A\text{ and }C$ and $\angle AOC=45°.$

The area of the shaded portion is _____ ${\text{cm}}^2\text{.}$

Circles of radius $10\text{ cm}$ and $6 \text{cm}$ overlap as shown:

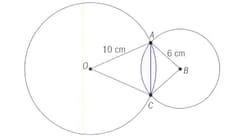
The circles meet at point $A\text{ and }C$ and $\angle AOC=45°.$

The value of $\angle ABC$ from the figure is _____ degrees. (correct upto $2$ decimals)

Circles of radius $10\text{ cm}$ and $6 \text{cm}$ overlap as shown:

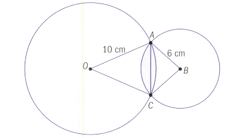
The circles meet at point $A\text{ and }C$ and $\angle AOC=45°.$

The length of the straight line segment joining $A \text{to }C$ is _____ cm.

The value of $x$ is_____?

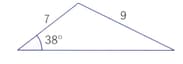
Use sine rule or cosine rule to find the marked sides and angles. Give answers correct to $3$ s.f.

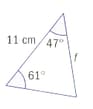
Use the sine rule or cosine rule to find the marked sides and angles. Given the answers correct to $3$ s.f.

Use the sine rule or cosine rule to find the marked sides and angles. Give answers correct to $3$ s.f.

Use the sine rule or cosine rule to find the marked sides and angles. Give answers correct to $3$ s.f.

Use the sine rule or cosine rule to find the marked sides and angles. Give answers correct to $3$ s.f.

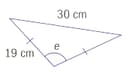
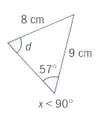
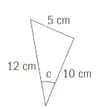
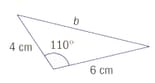
Use the sine rule or cosine rule to find the marked sides and angles. Give answers correct to three significant figures.